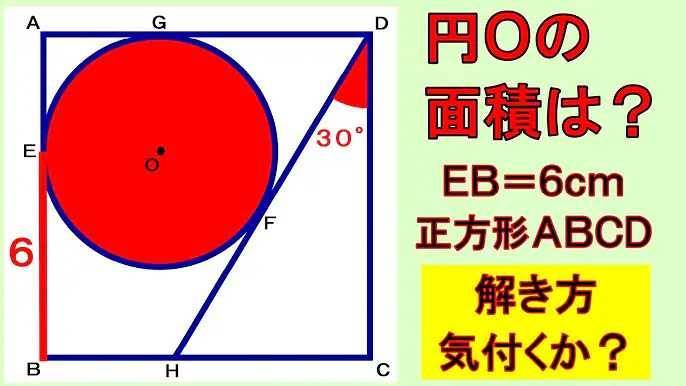
正方形の中の円の面積を求める方法、気付きますか？解けますか？この問題、ぱっと見ただけでは「難しい！」と思うかもしれません。でも、ちょっと図形の性質に目を向ければ、意外とシンプルに解けちゃいます！さあ、解いてみましょう。まず、正方形の中にきれいに収まっている円を想像してください。この円が正方形の辺に接しているということは、円の直径は正方形の一辺の長さと同じです。つまり、円の半径は「正方形の辺の長さの半分」ですよね。次に、円の面積を求める公式に進みます。円の面積は「半径×半径×π」です。この公式を使って、正方形の辺の長さがわかれば計算は簡単！仮に正方形の辺の長さを「a」とすると、円の半径は「a/2」。したがって円の面積は「(a/2)×(a/2)×π」、つまり「(a²/4)×π」となります。