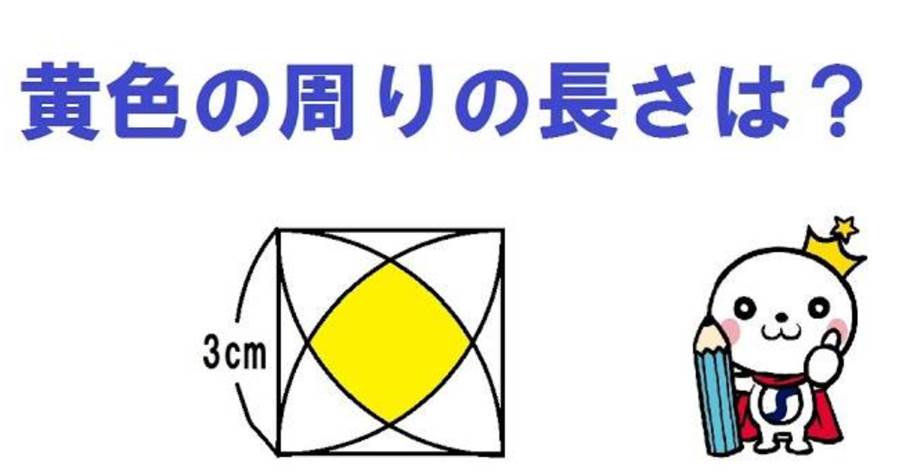
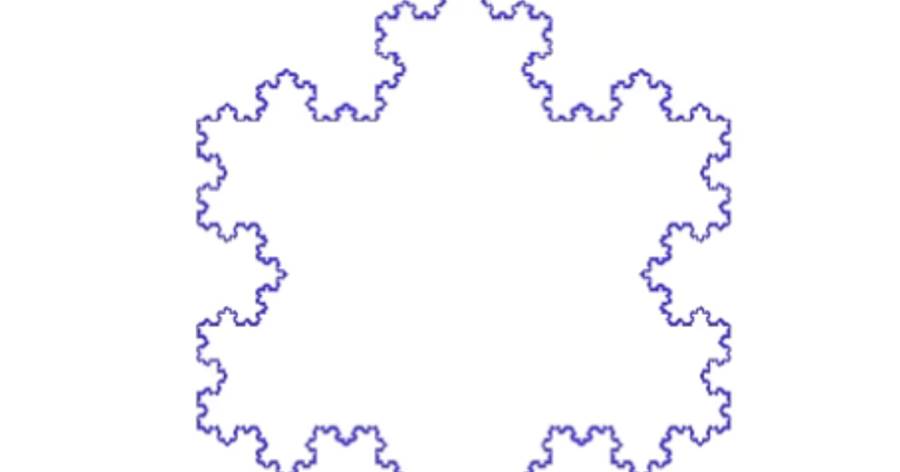
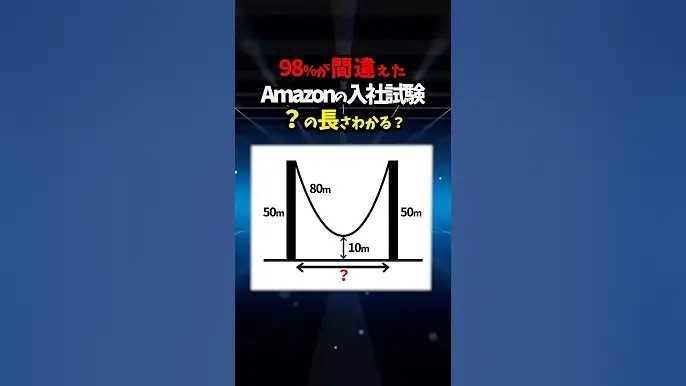
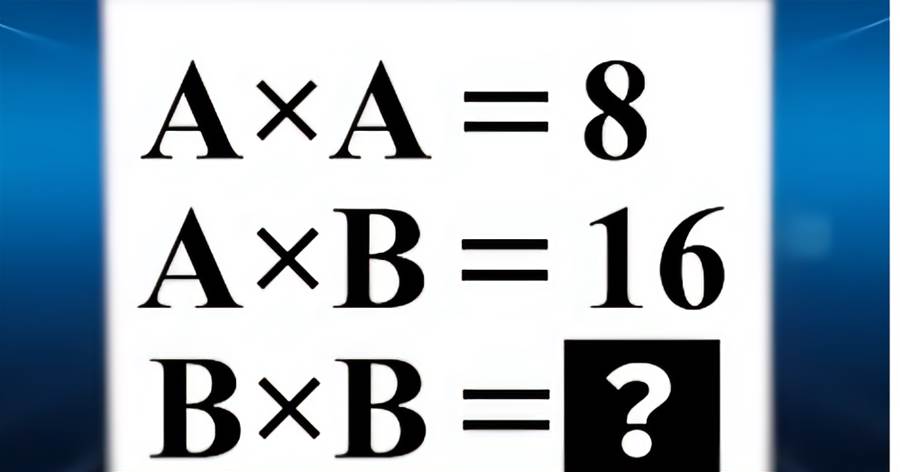義付が提示したこの数学の問題は、一見すると中学生でも理解できそうな簡単な内容ですが、意外にも奥深い仕組みを持っています。この問題の核心は、ある図形の面積を求めるというものです。情報として与えられるのは、逆品がある円の中の一辺の長さ。音楽型の面積は、大きい円から小さい円を引いたことによって求められます。大円の半径と小円の半径が知られているとして、それに基づき円周率を用いて、それぞれの円の面積を計算します。この問題が魅力的なのは、多角的な関係性の中で絶妙な挑戦を与えてくれる点です。国の推薦によって、共分される角度を理解することが鍵になります。そして、国別の要素で生じる変数を用いて、式を変形すると解が見えてくる仕組みになっています。最終的には答えに到達できる面積が求まるまでの過程がこの問題の面白さを際立たせていると言えるでしょう。