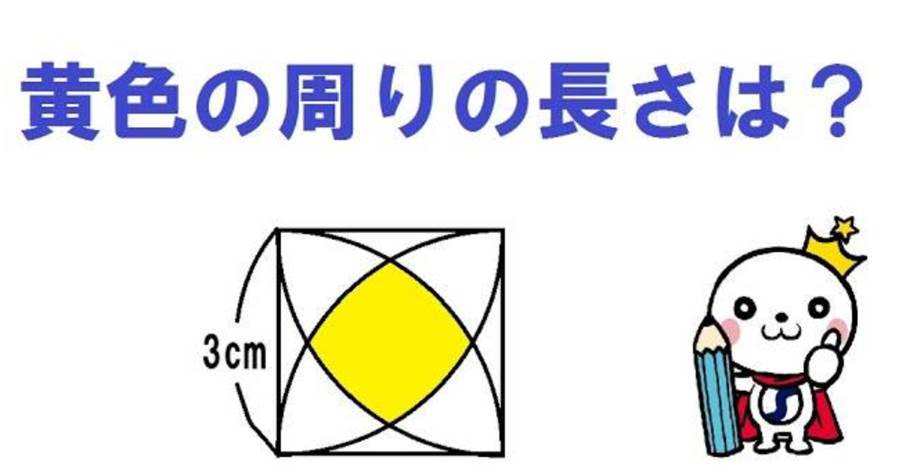
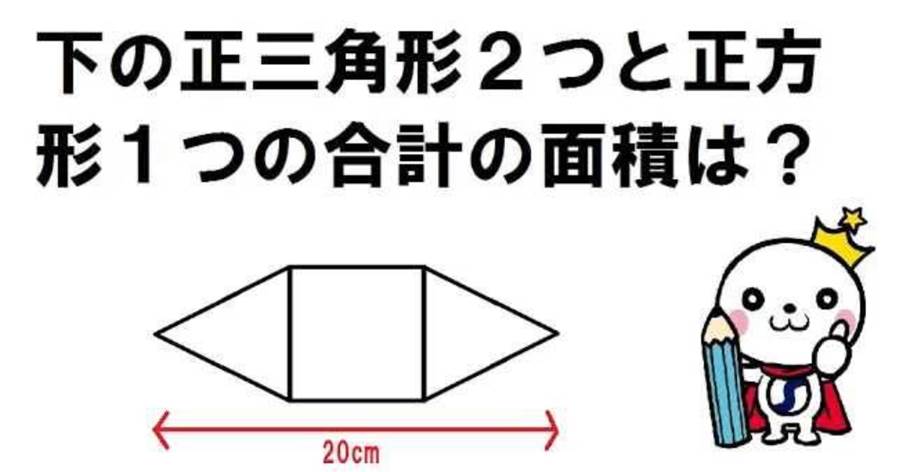
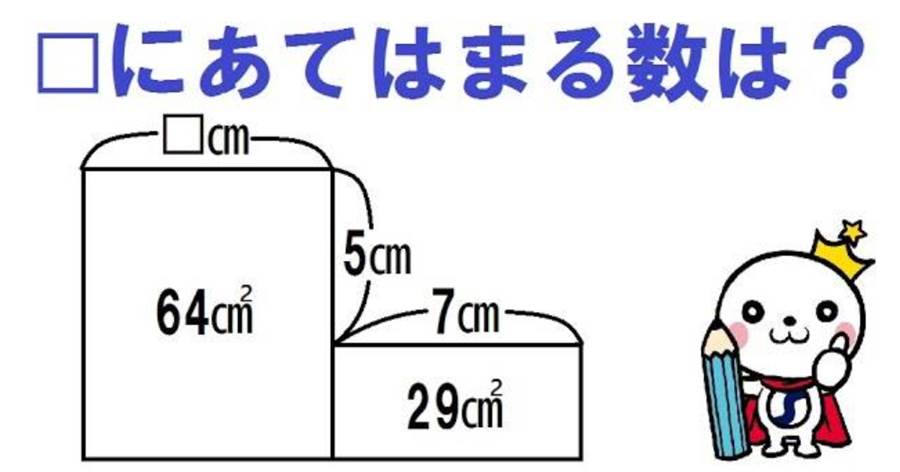
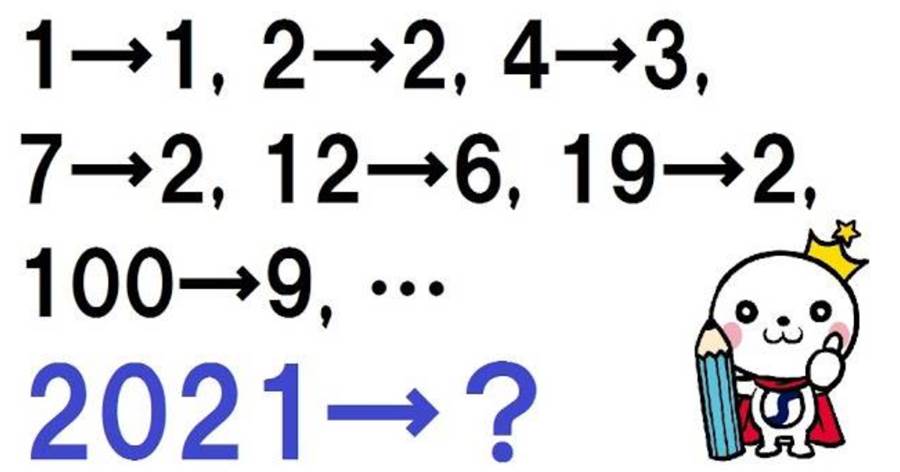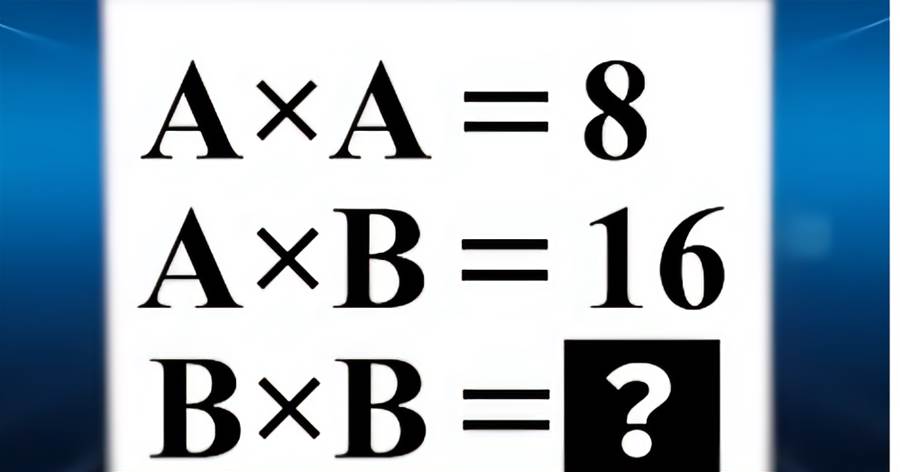数学の世界は無限の可能性を秘めていますが、時には子供でも解けるのに大人が頭を抱えてしまう問題も存在します。今回の挑戦は、そんなユニークな問題の一つです。ある正方形があります。その各頂点からコンパスで円を描き、その円が交わる部分を取り囲む長さを求める問題です。この問題はただの計算問題ではなく、図形の性質と円周率を使う必要があります。円周率を3.14として計算を進めます。問題の核心は、正方形の頂点から描かれた複数の円の交点に生じた弧の長さを求めることです。弧の中心角が30度であるため、円周を360度とした場合の割合で計算します。各円の半径が3センチの場合、求めた弧の長さは1.57センチとなります。それを四箇所分求めることで、合計6.28センチという結果が得られます。このように思わぬアプローチが必要な問題こそ、数学の醍醐味と言えるでしょう。